We recommend that all students seeking a diploma be required to ... [take] three years of mathematics. The teaching of mathematics in high school should equip graduates to ... understand geometric and algebraic concepts.—A Nation at Risk
In response to this call, many states including Louisiana, Mississippi, and North Carolina, and a number of school districts, including Washington, D.C., have established algebra as a graduation requirement.
Another approach with a similar result but a different rationale is The College Board's Equity 2000. This project calls for the elimination of tracking and the implementation of a college preparatory curriculum for all students as a way to address the inequity for non-college-bound students inherent in high school programs. While algebra is not a stated graduation requirement, all students take algebra. Six districts—Forth Worth, Texas; Milwaukee, Wisconsin; Nashville, Tennessee; Prince George's County, Maryland; Providence, Rhode Island; and San Jose, California—are participating.
Whether the goal is equity or increased mathematical achievement, “algebra for all” is a frequently expressed goal in the literature on school mathematics reform. But enrolling all students in algebra may be counterproductive. According to a recent report from the National Council of Teachers of Mathematics, “Algebra for everyone” has become a main thrust of many curricular reforms. In many cases, this is an algebra that is essentially the algebra of earlier decades and not an algebra that will prepare students to enter [our] vibrant and technological world (1993).
Algebra's reputation as arcane is well known and well deserved. The core of secondary school mathematics programs, algebra in its present form filters large numbers of students from the further study of mathematics. It consists of obscure topics, isolated from meaningful applications, and approached in a manner too abstract for most students. This abstraction is exemplified by the following exercise from a contemporary first-year algebra textbook:
Figure
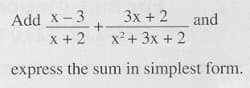
express the sum in simplest form.
Lynn Steen, the executive director of the Mathematical Sciences Education Board and a strong proponent of school mathematics reform, warns against algebra for all if that algebra is traditional (1992): Let's face it. For most students the current school approach to algebra is an unmitigated disaster.... On this the mathematics education community and its critics agree: first-year algebra in its present form is not essential for a quality mathematics education. This is not to say that algebra is not essential.
Achievement in algebra, even among students who have completed and passed it, is abysmal. According to the 1990 National Assessment of Educational Progress, 83 percent of the nation's 12th graders reported they had taken one year of algebra and 56 percent had taken two. Nevertheless, Fewer than half the high-school seniors (46 percent) demonstrated a consistent grasp of decimals, percents, fractions, and simple algebra, and only 5 percent showed an understanding of geometry and algebra that suggested preparedness for ... relatively advanced mathematics (Mullis et al. 1991).
- Algebra must be part of a larger curriculum that involves creating, representing, understanding, and applying quantitative relationships. Algebra should begin at an early age, extend to concepts traditionally viewed as calculus, engage a wider set of analytical tools, and connect to a wide variety of domains.
- The algebra curriculum should be organized around the concept of function. Functions are expressions of patterns and regularity and, as such, embody the essence of mathematics.
- New modes of representation need to complement the traditional numerical and symbolical forms. Historically, algebra has used a formal propositional language that served a small elite. New media allow visual, graphic representations of relationships that are likely to be more easily learned and used by an enlarged segment of the population.
- Algebraic thinking, which embodies the construction and representation of patterns and regularities, deliberate generalization, and most important, active exploration and conjecture, must be reflected throughout the curriculum across many grade levels.
Algebra for all is the right goal at the right time. We just need to get the right algebra.
