Mathematics textbooks are a staple in U.S. classrooms. Teachers use them daily to plan and deliver lessons; students work exercises in them and carry them home, conveying to parents the activity of the mathematics classroom. In 2001–2002, K-12 school districts spent more than $4 billion on textbooks (Education Market Research, 2002), making it one of the largest school expenditures, with the exception of teacher salaries.
Textbooks represent a substantial financial investment and strongly influence what students learn. They can easily facilitate—or compromise—comprehension. So who decides what goes into mathematics textbooks? What checks and balances ensure that teachers are providing students with high-quality materials?
A Test on Textbooks
Schools typically adopt new mathematics textbooks every five to seven years.
Before publishing and distributing new textbooks to schools, textbook developers field-test and revise new materials on the basis of evidence of effectiveness.
Textbook authors and publishers base the content of mathematics textbooks on national curriculum standards.
U.S. textbooks resemble textbooks used in countries where students perform well on international mathematics assessments.
Mathematics textbooks have a direct impact on what schools teach and what students learn.
Schools typically adopt new mathematics textbooks every five to seven years.
True. The five- to seven-year cycle allows for various disciplines, such as science, language arts, and social studies, to regularly select new textbooks while distributing their cost somewhat evenly from year to year. Schools replace textbooks because the textbooks deteriorate physically and because teachers revise their instructional approaches or modify the emphasis on content. In general, however, U.S. schools do not adopt new mathematics textbooks in a given month or year. This means that textbook publishers must produce continuously marketable materials for states or school districts with different adoption timelines.
Before publishing and distributing new textbooks to schools, textbook developers field-test and revise new materials on the basis of evidence of effectiveness.
False. Two factors generally preclude textbook publishers from field-testing new material: the high cost of developing and publishing a new textbook series—in excess of $20 million for a complete K-6 mathematics textbook series—and the need to produce materials for varied markets under tight timelines. In addition, consumers rarely demand proof that commercially generated materials are indeed effective. Publishers sometimes test new materials with teachers, but this assessment generally relates to the physical design of the textbook rather than to content or pedagogical approach. Most publishers do not gather scientific evidence regarding the effectiveness of the textbook during its development or during its use in the classroom. The result is that textbooks, a potential change agent for improving student learning, generally undergo few, if any, major changes from one edition to the next.
Textbook authors and publishers base the content of mathematics textbooks on national curriculum standards.
False. The United States, unlike most industrialized countries in the world, leaves the decision about what mathematics to teach and when to teach it to local control. At the state or local school district level, individual teachers or committees of teachers, administrators, and parents make decisions about course content. The federal government does not provide national curriculum standards to guide local decision making. The National Council of Teachers of Mathematics (NCTM), a nonprofit organization of teachers, has produced a K-12 curriculum framework for mathematics. This framework, Principles and Standards for School Mathematics (2000), presents general guidelines for mathematics learning expectations in four grade bands (preK-2, 3–5, 6–8, and 9–12). Some publishers do take these guidelines into account when producing math textbooks.
U.S. textbooks resemble textbooks used in countries where students perform well on international mathematics assessments.
False. U.S. textbooks are unique in their size and amount of content covered. Authors and publishers tend to add topics to U.S. mathematics textbooks to meet various local and state curriculum requirements, but they rarely delete information to make room for new topics. The textbooks grow larger with each new edition. U.S. mathematics textbooks address substantially more information at each grade level than textbooks used in countries where students perform well on international assessments, such as Japan and Singapore. Also, U.S. secondary schools have historically organized school mathematics courses into separate content strands, such as algebra, geometry, statistics, and calculus. Schools outside the United States, however, typically integrate mathematics so that students study algebra, geometry, and statistics every year.
Mathematics textbooks have a direct impact on what schools teach and what students learn.
True. Tyson-Bernstein and Woodward (1991) note the ubiquitous nature of textbooks in U.S. schools; textbooks are a prominent, if not dominant, part of teaching and learning. This phenomenon, however, is not limited to the United States, as international studies indicate (Robitaille & Travers, 1992):Teachers of mathematics in all countries rely heavily on textbooks in their day-to-day teaching, and this is perhaps more characteristic of the teaching of mathematics than of any other subject in the curriculum. Teachers decide what to teach, how to teach it, and what sorts of exercises to assign to their students largely on the basis of what is contained in the textbook authorized for their course. (p. 706)
Because teachers often use the textbook as their primary resource to plan daily mathematics instruction (Weiss, Banilower, McMahon, & Smith, 2001), the textbook has come to play three crucial roles. First, it determines how the teacher will sequence material. In a 2nd grade mathematics textbook, for example, early chapters focus on place value as a fundamental structure of the number system. Students need to understand this concept before they can learn to add or subtract multidigit numbers. Likewise, an algebra textbook introduces students to techniques for solving linear equations in one variable before considering more complex equations.
In addition to presenting mathematics in a particular sequence, the textbook also suggests the content that teachers should teach. This factor is particularly significant when we look at U.S. mathematics textbooks, which address many different topics superficially and repeat material from earlier grades. This situation is the result of a lack of national consensus on a specific mathematics curriculum for each grade level.
Consider the following disparity: A 4th grade mathematics textbook in the United States averages 530 pages, whereas the average number of pages in a 4th grade mathematics textbook in other countries participating in the Trends in International Mathematics and Science Study (TIMSS) is 170 (Schmidt & Valverde, 1997). According to the TIMSS textbook analysis (Schmidt, McKnight, & Raizen, 1997), U.S. mathematics textbooks have a significant amount of repetition and introduce only one or two new topics each year from 4th to 8th grade, whereas other countries introduce between six and seven new topics during this period. Excessive repetition of material leads to shallow treatment of mathematics and fails to stimulate student interest or challenge student thinking.
Textbooks' third crucial role is to provide the teacher with activities and instructional ideas for engaging students in the topics presented. Textbooks serve as a set of lesson plans for the teacher, complete with sample problems, diagrams, worked-out examples, and homework assignments. The number of pages that the textbook allots to a specific topic influences the amount of time that the teacher spends on that topic (Chávez, 2003). Not surprisingly, the teacher often mirrors the textbook's method of presentation.
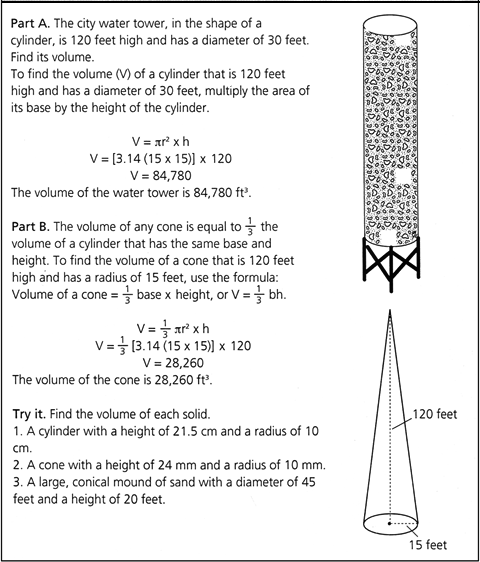
Consider a typical textbook lesson for 7th or 8th graders on the topic of the volume of cylinders and cones. Figure 1 shows how U.S. textbooks have presented the topic over the past two decades. The lesson begins with a real-life problem: finding the volume of the city water tower, which is in the shape of a cylinder. The lesson presents the topic, shows the solution, and includes similar problems for students to solve. Notice that the textbook lesson presents one formula for determining the volume of a cylinder and a different one for determining the volume of a cone. The lesson presents each formula as a discrete fact to remember rather than discussing the connection between these two formulas or to material previously studied.
Figure 1. “Traditional” U.S. Textbook Lesson: Volume of Cylinders and Cones
The textbook method of presentation necessarily affects instruction. Stigler and Hiebert (1999) characterize the typical 8th grade mathematics lesson in the United States as “learning terms and practicing procedures” (p. 27). According to the researchers' analysis of videotaped lessons, U.S. teachers usually follow a routine that begins with short-answer review questions followed by relatively long segments of homework checking. After checking the homework, the teacher presents the students witha few sample problems and [demonstrates] how to solve them. Often the teacher engages the students in a step-by-step demonstration by asking short-answer questions along the way. (p. 80)
The teacher then asks the students to work on problems similar to those already demonstrated. A homework assignment with more practice problems concludes the lesson.
Given the limited preparation in mathematics of most elementary teachers and the shortage of teachers certified to teach mathematics at secondary schools, the mathematics textbook becomes the mathematics program for a large segment of the teaching corps.
A Better Alternative
Until recently, most mathematics textbooks looked alike. Their tables of contents were often indistinguishable. From 3rd grade mathematics to 9th grade algebra, textbooks followed the same pattern: Each instructional unit consisted of a few sample exercises that the teacher demonstrated, followed by a set of exercises for students to work on. A two-page spread typically conveyed this mathematics “lesson.” The textbook provided the main components of the daily lesson plan; teachers needed only to cover the material and perhaps supplement it occasionally to add interest and facilitate student mastery of the topic.
Textbooks in the United States typically present mathematical ideas as facts to memorize rather than as meaningful relationships. Not all U.S. mathematics textbooks are alike, however. Sparked by U.S. students' lower-than-expected performance on national and international assessments, the National Science Foundation launched a major initiative to create new mathematics textbooks based on challenging mathematics curriculum standards and instructional strategies aligned with current research on learning (NCTM, 1989, 2000). This initiative has produced textbooks at the elementary, middle, and high school levels that break the mold of traditional instruction (Reys, Robinson, Sconiers, & Mark, 1999; Trafton, Reys, & Wasman, 2001).
Skills remain a central theme in the new textbooks, but teachers introduce these skills in real-world contexts that enable students to investigate and solve problems. At present, approximately 10–15 percent of U.S. classrooms use these “standards-based” textbooks. They differ from traditional mathematics textbooks in that they present mathematical ideas in various contexts and engage students in exploring ideas, solving problems, sharing strategies, and building new knowledge based on solid conceptual understanding. Teachers no longer simply “cover” material. Rather, they facilitate a classroom learning environment that encourages questioning, conjecturing, and problem formulation and values student thinking and multiple strategies.
Consider an alternative textbook presentation on the topic of finding the volume of cylinders and cones. The lesson spans several days of instruction and approximately six pages in the mathematics textbook. Early in the lesson, students focus on developing a formula for finding the volume of a cylinder, calling on familiar models previously studied (see fig. 2). Once the students have studied this concept, they investigate the relationship between the volume of a cone and the volume of a cylinder by building paper models of both, estimating volumes, and then confirming volumes by actually filling both containers with dry ingredients and measuring their results. The textbook then poses the following questions: What appears to be the relationship between the volume of a cone and the volume of a cylinder with like dimensions? Does this relationship hold for larger or smaller cones and cylinders?
Figure 2. “Standards-Based” Textbook Lesson: Volume of Cylinders and Cones
This textbook lesson uses a particular instructional approach. Students build and evaluate models, make and test conjectures, and build on prior learning. The teacher orchestrates discussion and summarizes the findings. At the end of the lesson, students have the tools needed to solve problems in this topic area. Such instruction, which emphasizes exploring mathematical relationships and making connections, is far more likely to help students understand mathematics than is a lesson that simply provides students with a formula. Rather than “covering” topics, teachers help students “uncover” important mathematical ideas that they need to learn and understand.
Recent studies confirm the value of these standards-based mathematics textbooks (Reys, Reys, Lapan, Holliday, & Wasman, 2003; Riordan & Noyce, 2001). Researchers compared student performance in school districts using standards-based mathematics curriculums for at least two years with the performance of students from similar backgrounds in districts using traditional mathematics textbooks. The findings indicate that students using the standards-based curriculums scored as well as or significantly higher than students using other materials. These results were consistent across all subgroups of students.
Selecting a Textbook
Given the prominent role of mathematics textbooks, making a wise selection is crucial because it determines the scope of mathematics that students experience and, to some extent, how teachers present the material and how students learn. Several reports (Blank, Earle, Schmidt, Roseman, & Nohara, 1997; Kulm, 1999; NCTM, 1981; NCTM & ASCD, 1991) identify various criteria for evaluating and selecting mathematics textbooks. Teachers and administrators involved with selecting mathematics textbooks should be familiar with the characteristics associated with standards-based mathematics curriculums (Trafton, Reys, & Wasman, 2001): Textbooks should present material coherently, develop ideas in depth, promote sense making, engage students, and motivate learning.
What key mathematical ideas in each content strand should each grade level address?
How does the content of the textbook align with these key mathematical ideas?
What types of activities does the textbook provide? Are students challenged to think and develop understanding, or are they simply shown how to work some exercises and then asked to practice procedures? Will these activities engage students in mathematical thinking and activity?
Is there a focus on mathematical thinking and problem solving? Are students expected to explain “why”? Does the textbook encourage students to explore “what if” questions and to offer and test conjectures?
What About Professional Development?
Strong professional development should accompany the adoption of a new textbook so that teachers understand the textbook's goals and strategies. Research has shown that the process of investigating and implementing curriculum, such as the curriculum inherent in a new textbook, can enhance a teacher's knowledge of the subject matter and improve instruction (Ball & Cohen, 1996; Reys, Reys, Barnes, Beem, & Papick, 1997).
The selection and successful implementation of standards-based mathematics textbooks require a professional development plan that includes an initial introduction to the materials, followed by regular opportunities for teachers and administrators to meet and discuss accomplishments and challenges. Providing opportunities for teachers to collaborate on previewing upcoming curriculum units and to interact with experienced users of the curriculums contributes to strong implementation and ongoing professional growth.
Teaming Up for Success
It takes a strong team to wisely choose and implement mathematics textbooks. This team should include the principal, teachers, and parents. Each has a special role in the process.
The principal needs to provide leadership in establishing clear learning goals in mathematics. He or she not only facilitates the selection of good textbook materials but also ensures that teachers are kept informed about current mathematics curricular alternatives. The principal should provide time for teachers to meet and study the textbooks. He or she should encourage teachers to attend specialized workshops on promising curriculums and to test materials in their classrooms and share their experiences.
Teachers need to commit themselves to supporting all students in learning mathematics and to being open to change if current techniques and resources do not meet this challenge.
And parents need to be aware of the mathematics topics that their children will be learning. Involving parents in a specific mathematical activity drawn from the textbook during a school “Math Night for Parents” will help them better understand and appreciate the level of mathematical activity that their children will regularly encounter in the classroom.
Wise selection of mathematics textbooks, coupled with successful implementation, will contribute to the mathematical learning of students and to the professional growth of their teachers.