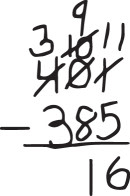This title sounds, well, dramatic. But pause to think about a world crisis. Take global warming, for example: How did we recognize the world was getting warmer? Mathematics. Mathematics helps us identify problems and helps us solve them. Beyond global issues, everyday living involves financial literacy, interpreting data, and basic computation—all elements of mathematics.
Yet, the traditional approach to teaching mathematics in schools has been to teach skills now so that students can apply them later to authentic learning. The impact of this approach is that far too few adults feel confident in mathematics and far too few develop competence in mathematics (Aguilar, 2021; Hart & Ganley, 2019; U.S. Department of Education Institute of Education Sciences, 2020). To fix this, we need to reimagine mathematics learning experiences with an eye on the future. That means extinguishing some long-standing cultural practices in mathematics classrooms, and replacing them with practices that reflect the reasoning and decision-making that define mathematics as a discipline. This reimagined approach increases competence, because students are actually doing mathematics (which goes well beyond remembering processes) and confidence, because confidence comes from realizing you can figure out a problem without needing someone to show you how to do it.
STEM Disciplinary Practices in the Classroom
Disciplinary practices for mathematics, like science, involve students doing what professionals in STEM disciplines do. STEM professionals rarely imitate what someone has shown them how to do, and regularly are positioned to figure something out. In his 2013 book The Case for STEM Education: Challenges and Opportunities, Rodger Bybee explains, “The purpose of STEM education is to develop the content and practices that characterize the respective STEM disciplines” (p. 4). These disciplinary practices are best described in the Standards of Mathematical Practice (CCSSO, 2010) and the Science and Engineering Practices (NGSS Lead States, 2013) as listed in Figure 1.
These practices emerged from an analysis of what scientists, engineers, and mathematicians do as they determine things such as how to predict global warming trends, analyze traffic patterns or airline flight schedules, assess safe bridges, and understand countless other problems. Yet to become competent and confident in these disciplines, the practices should also define what students do on a daily basis in math and science classes. In a nutshell, students should be thinking and making decisions as STEM professionals do, whether students are solving real-life problems or learning to subtract whole numbers.
The mathematical practices in Figure 1 can be unpacked into observable student actions that we can look for in a classroom. Those actions include:
Students choose how to solve a problem.
Students choose representations and tools to support their reasoning.
Students notice patterns and structures and use them to solve problems.
Students justify their processes and their answers.
Students reflect on their answers and decide if they make sense.
Unfortunately, these actions are rarely prioritized in schools, despite their appearance in state standards. The pressure to perform well on end-of-year exams has resulted in an emphasis on grade-level content standards. Students are not doing mathematics (i.e., engaging in any of the mathematical practices), they are just learning about mathematics (i.e., this is how to solve for x). Not only is the learning-about approach a missed opportunity to develop disciplinary practices, but it also misses the mark in terms of developing mathematical fluency.
What Is Mathematical Fluency?
When people hear “fluency” they might think of basic facts or algorithms. But mathematical fluency, formally called procedural fluency, is actually “skill at carrying out procedures flexibly, accurately, efficiently, and appropriately” (National Research Council, 2001). Let’s look at the difference between an approach to mathematics learning that prioritizes following steps in an algorithm and one that encourages fluency.
Consider ways to solve the problem 401 – 385. The method that is typically prioritized in schools is to stack and subtract each place value, starting with the ones place and regrouping as needed. It looks like this:
A mathematically fluent person, however, would not use this algorithm; instead, they would notice that both numbers are close together and would figure out how far apart they are (e.g., “I counted up 385 to 400 is 15, and one more is 16”). This is a more fluent approach to solving the problem because it demonstrates flexibility (it was chosen based on the numbers in the problem), efficiency (could be done mentally and more quickly than other options), and accuracy (the answer is correct). Figure 2 illustrates these three fluency components, along with actions that reflect the components.
The overemphasis on algorithms and a narrow focus on accuracy has unfortunate implications for our students. When students only learn about mathematics, they:
Don’t understand mathematics (Why are we crossing out and regrouping?).
Develop anxiety (I might forget the steps, I might be wrong, that will be embarrassing).
Don’t feel like they are good at mathematics (I’m making mistakes, other students are faster than me).
What is the future for these students?
They don’t like mathematics (I don’t like this feeling of being wrong, and I see other students are faster, and therefore smarter, than I am).
They don’t want to pursue mathematics (I am not going to take math my senior year of high school and/or in college).
They don’t pursue STEM professions (I wanted to become a ___ but I had to take too many math courses).
In contrast, a focus on procedural fluency can be empowering. Ask one or more students, “How might you solve 48 + 49?” Listen to their ideas and look at their faces—you will see the emergence of mathematical competence and confidence as they start brainstorming different ways to solve the problem. (Try it!) In this approach, the mathematical practices are present: students attend to the structure of the problem, reason abstractly and quantitatively, and explain their thinking.
A key difference is removing the idea that students must remember only one way to solve a problem. Instead, students are invited to make choices among multiple ways to solve it. And, this is the very kind of thinking that is required in considering real problems, from personal family finance to addressing national debt, maintaining forests, or reducing our ecological footprint. For every challenge, there are multiple solution pathways, with various considerations that must be taken into account. In positioning students as decision-makers as they engage in mathematics, they are developing the mathematical skills to solve global problems, as well as the disposition to be a problem solver.
Let’s extinguish the statement 'I was never good at math,' which actually means, 'I was not good at remembering processes that had no apparent purpose.'
Mathematics Experiences to Extinguish
To grow competent, confident students, there are several long-held practices in mathematics teaching and learning that we have to extinguish. This is not a complete list, but it is an important list. As you read, consider how you might garner support for removing these from your school, district, or other setting:
1. Memorizing. Memorization is not effective for learning and retention. In 2010, the Program for International Student Assessment (PISA) assessed the mathematical learning strategies of more than 250,000 15-year-old students in 41 countries, looking for correlations with achievement (OECD, 2010). They found that “memorization/rehearsal strategies are almost universally negative, suggesting that memorization is an ineffective strategy for learning mathematics” (p. 99). Memorizing says to students, “No need to make sense of math.” Having students memorize basic facts is particularly damaging because they lose out on the opportunity to develop essential number relationships that will support their fluency beyond basic facts (Bay-Williams & Kling, 2019).
2. Speed/timed activities. Children as young as 1st grade experience anxiety in math (Ramirez, Shaw, & Maloney, 2018). Extinguishing timed basic fact tests could go a long way in lessening that anxiety. Board races as well as apps and games that position the faster thinker as the winner must go. As Figure 1 emphasizes, automaticity with basic facts—not speed—is the goal. Pressure to recall a fact quickly doesn’t make a student automatic—it makes them anxious.
3. Teacher shows how to solve a problem, students replicate. An “I do, we do, you do” approach to mathematics is the opposite of the disciplinary practices approach in mathematics and science, both of which are inquiry-based fields. Familiarity with and understanding of algorithms is important, but weeks spent working on standard algorithms, at the exclusion of other methods, is malpractice. “I do, we do, you do” is the predominant way that math is learned in school, especially middle and high school. This will be difficult to extinguish, but if these days were pared down to, say, less than half, and the other days were designed in ways that prioritized the mathematical practices, the impact on student competence and confidence could be profound.
Mathematics Experiences to Expand
We now know what needs to be extinguished. But what needs more attention in preK–12 classrooms? And how can these approaches support procedural fluency? This is not a complete list, just a recommended place to start. To illustrate, here are three examples (from basic facts to algebra). As you take a look, ask yourself, How might a fluent person solve these problems?
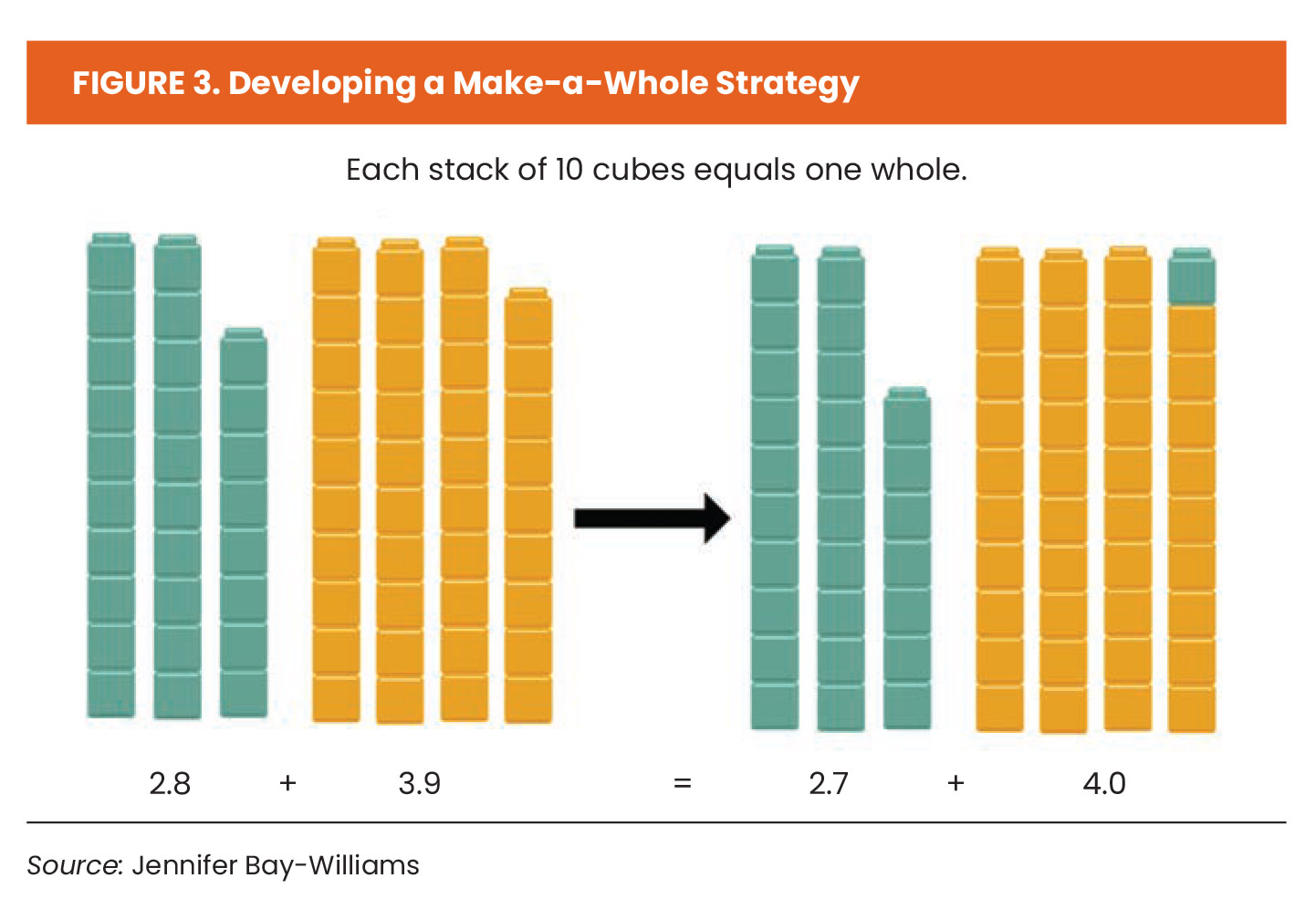
1. Teach students to use reasoning strategies. Reasoning strategies involve choice and reasoning. To solve for 9 + 7, for instance, there are several good options. One is “Making a Ten.” Move 1 from the 7 to the 9 to create a new expression 10 + 6. The answer is 16. This strategy is based on knowing how far away a number is from 10, which is a fundamental understanding in mathematics. So, in teaching strategies, you are developing strong conceptual foundations. Can that strategy be used for 2.8 + 3.9? Yes, it can! Now, we are “Making a Whole.” Move 0.1 from 2.8 to 3.9 to create the expression 2.7 + 4. The answer is 6.7. Mathematics educators teach this strategy using manipulatives, visuals, and stories, as illustrated in Figure 3.
2. Teach students to choose among strategies (and algorithms). Many students think that once they learn the standard algorithm, they are supposed to always use it. Instead, standard algorithms should be thought of as an addition to a student’s existing repertoire of strategies (Bay-Williams & San Giovanni, 2021). Within that repertoire, a student’s job is to notice features of a problem to help them make an appropriate choice to solve the problem efficiently.
Take a look at 6(x – 1) – 4(x – 1) = 10. Rather than immediately “eliminating parenthesis first,” look at the features in this problem. The quantities inside the parenthesis are the same, so combining those two terms will be efficient. The new equation is 2(x – 1) = 10. At this point, relational reasoning can be applied (what can x be so that the quantity inside the parentheses equals 5? 6).
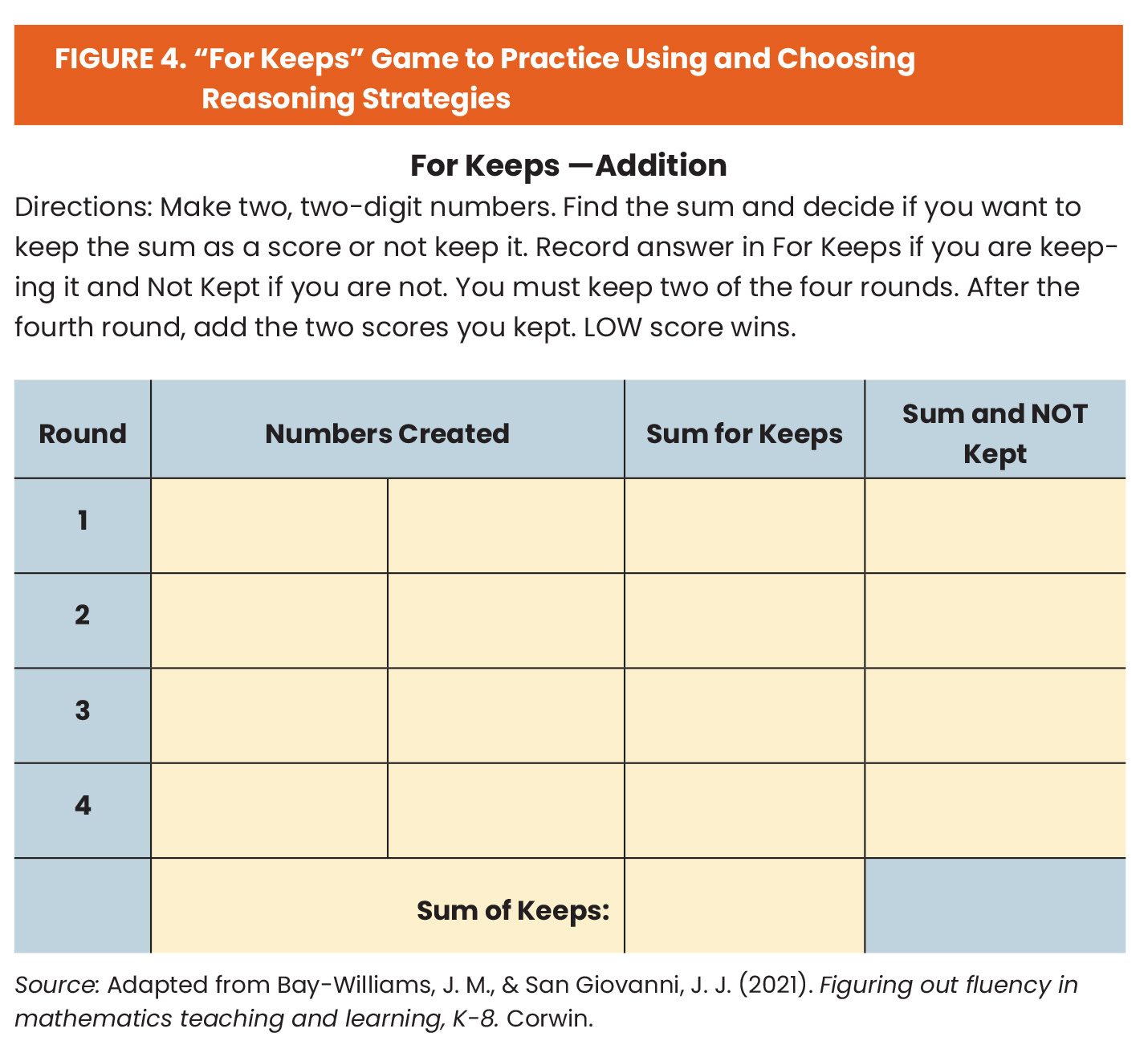
3. Practice reasoning strategies. Practice should involve reasoning, not replicating! Practice can be motivating and meaningful, especially with games. For example, you can have students play “For Keeps” (see Figure 4 for instructions), saying aloud the reasoning strategy to find the sum. If they draw 5, 2, 9, 4, and make the expression 29 + 45, they can use the “Make a Tens” strategy. This game can be adapted to decimals (2.9 + 4.5) to practice the “Make a Whole” strategy. “For Keeps – Subtraction,” similarly, can be used to practice subtraction reasoning strategies.
4. Attend to and assess fluency. Math tests are graded based on correct answers. That is an accuracy assessment, not a fluency assessment. How are flexibility and efficiency assessed? Prompts can be added to tests that focus on efficiency and flexibility. For example, trade out the instruction, “Solve using ___ method” for one of these options:
Choose your method for each problem.
Use at least three different strategies in solving this set of problems.
Select one problem and explain what strategy you used and why you chose it.
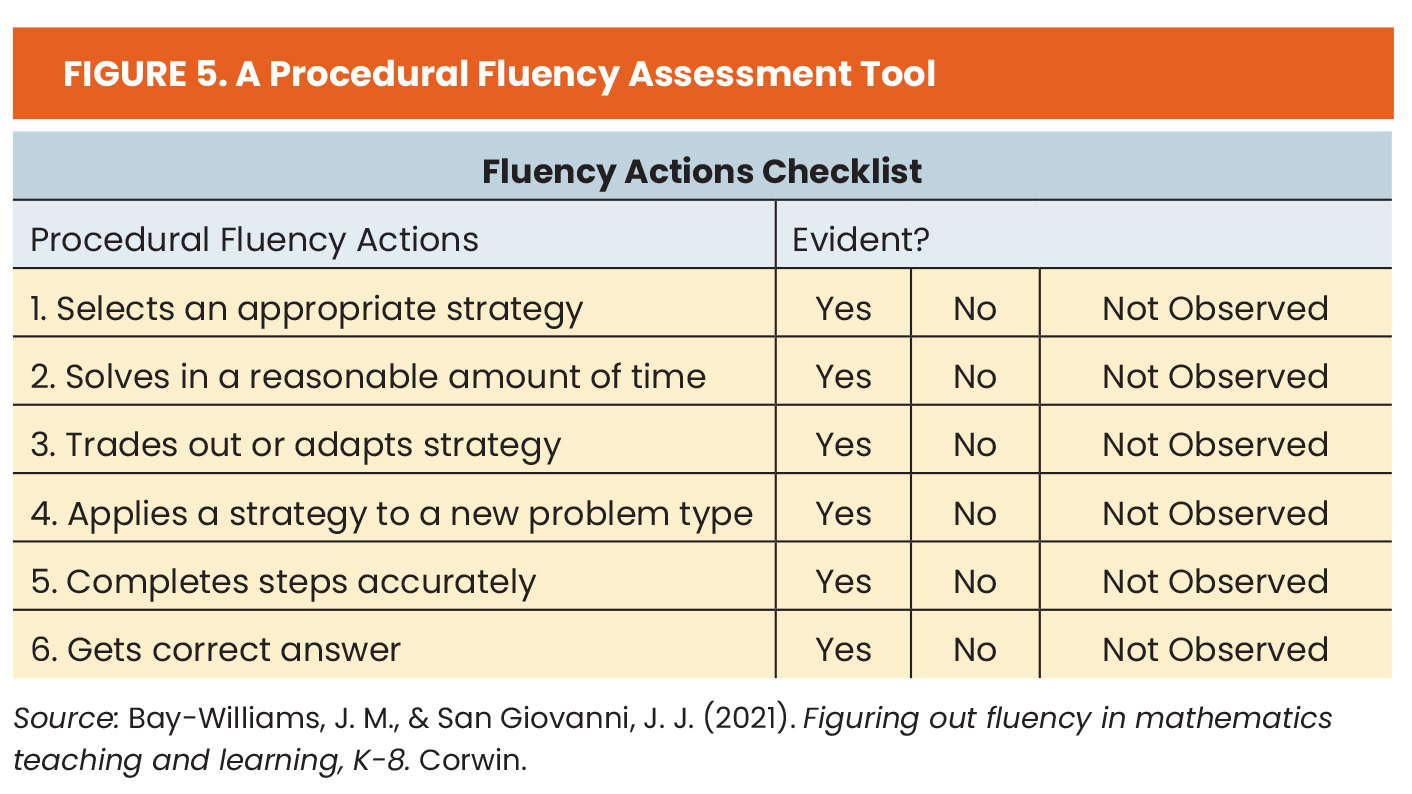
Other assessments can also better assess fluency, including interviews and writing prompts. The checklist in Figure 5 is one way to provide feedback on students’ emerging fluency. It could be attached to an adapted test or writing prompt or shared after an interview to communicate to students (and their caregivers) how they are developing as a mathematician. As the list is shared, help students and caregivers note the importance of actions 1–4 in the 21st century, positioning humans as decision-makers and recognizing that accuracy, while a component of fluency, is increasingly done by technology.
A key distinction in the reimagined classroom is student decision-making—students choose methods and reflect on their choices, changing them out as needed.
“I Was Never Good at Math”
When we swap memorization, speed drills, and replicating processes for opportunities to engage in the mathematical practices of the discipline, we are preparing mathematicians. A key distinction in the reimagined classroom is student decision-making—students choose methods and reflect on their choices, changing them out as needed. Hopefully these students will be more motivated to choose STEM professions. Increasing the number and diversity of students entering STEM professions strengthens the health professions, engineering, business, and, of course, K–12 teaching and leading. These professionals daily support the infrastructure of the world, ensuring a population of well-educated and healthy individuals in a safe and thriving society. Meanwhile, some of these STEM-enticed individuals will become researchers investigating the toughest problems the world faces. Whether students pursue a STEM profession or not, learning mathematics as decision-making better equips them to make sound decisions in their own finances and interpret world issues that are reported using statistics and other mathematics.
Meanwhile, let’s extinguish the statement, “I was never good at math,” which actually means, “I was not good at remembering processes that had no apparent purpose.” The more accurate statement is, “My math learning experiences didn’t prepare me to do math.” This can and must change. The future requires a population of confident, competent, and mathematically fluent decision-makers who can understand global challenges and take action to address them.
Math Fact Fluency
An indispensable guide for any educator who needs to teach basic mathematics facts from experts Jennifer Bay-Williams and Gina Kling.